Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls A-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Freier Fall mit Luftreibung
Inhaltsverzeichnis
1.1. Newtonsche Axiome und Strömungsarten
1.2. Reibungskraft, Reynoldszahl und Widerstandsbeiwert
1.3. Bewegungsgleichung und maximale Endgeschwindigkeit
1.4. Geschwindigkeit und zurückgelegter Weg
2.1. Ermittlung des Widerstandsbeiwertes
2.2. Berechnung der Reynoldszahl
3.1. Diskussion und Vergleich mit Literaturwerten
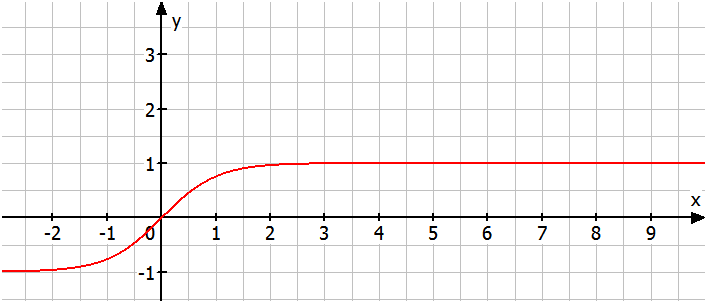
Abbildung 1: Grafische Darstellung der Tangens Hyperbolicus-Funktion
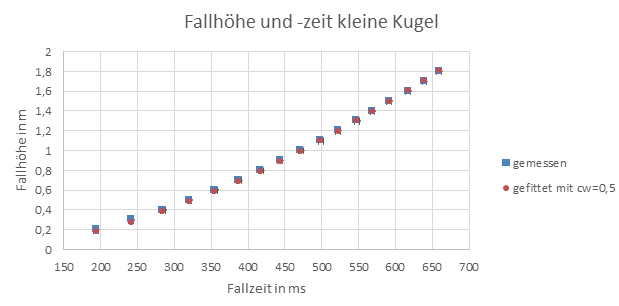
Abbildung 2: Fallhöhe und -zeit der kleinen Kugel
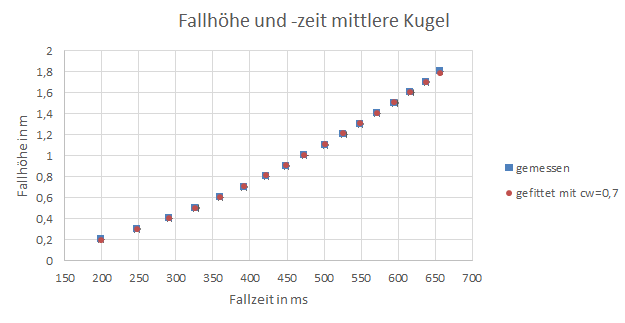
Abbildung 3: Fallhöhe und -zeit der mittleren Kugel
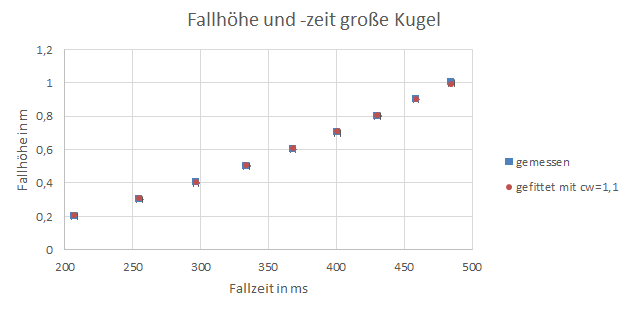
Abbildung 4: Fallhöhe und -zeit der großen Kugel
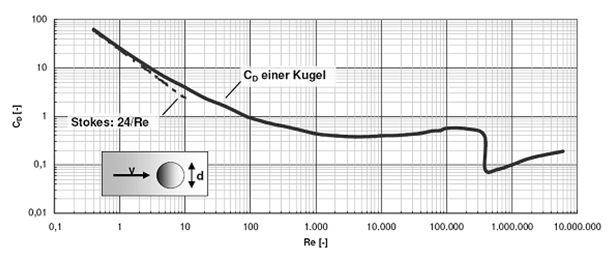
Abbildung 5: Widerstandsbeiwert für die entsprechenden Reynoldszahlen [2]
1.1. Newtonsche Axiome und Strömungsarten
1. newtonsche Axiom:
Jeder Körper behält seine Geschwindigkeit und Richtung so lange bei, bis er durch eine äußere Krafteinwirkung zu einer Veränderung gezwungen wird.
2. newtonsche Axiom:
Durch eine einwirkende Kraft F wird der Körper beschleunigt, wobei die Beschleunigung a proportional zu der wirkenden Kraft ist und deren Richtung besitzt:
(1.1.1)
3. newtonsche Axiom:
Wirkt ein Körper A auf einen Körper B mit einer beliebigen Kraft F, dann wirkt auch der Körper B auf Körper A mit der gleichen Kraft F. Allerdings sind die Kräfte dabei entgegengesetzt:
(1.1.2)
Es wird zwischen zwei Strömungsarten unterschieden. Die eine Art ist die laminare Strömung. Bei dieser findet während der Bewegung von Flüssigkeiten keine sichtbare Verwirbelung, beziehungsweise Querströmung, statt, sondern die Flüssigkeit strömt in Schichten, welche sich nicht miteinander vermischen. Die andere Art ist die turbulente Strömung. Dabei tritt eine sichtbare Verwirbelung der sich bewegenden Flüssigkeit auf und führt so zu einer starken Vermischung der einzelnen Strömungsschichten.
1.2. Reibungskraft, Reynoldszahl und Widerstandsbeiwert
Die Reibungskraft entsteht, in diesem Versuch, durch den, auf die fallende Kugel, wirkenden Luftwiderstand . Erzeugt wird dieser Widerstand dadurch, dass die Kugel während des Fallens durch die Luft, die Luftmoleküle beiseite drängen muss um nach unten zu gelangen und dabei an ihnen reibt. Die Formel zur Berechnung Reibungskraft wird hergeleitet mittels der kinetischen Energie, über welche jeder sich bewegende Körper verfügt:
(1.2.1)
wobei m der Masse und v der Geschwindigkeit entspricht. Und der, entgegen der kinetischen Energie wirkenden, Arbeit W:
(1.2.2)
dabei ist ds der Weg, welcher zurückgelegt wird. Des Weiteren ist die Masse eines Körpers auch definiert als:
(1.2.3)
und das Volumen V als:
(1.2.4)
wobei A die Querschnittsfläche des fallenden Körpers und Dichte des Fluides ist. Setzt man nun die Gleichungen (1.2.1) und (1.2.2) gleich, stellt um und fügt dann die Gleichungen (1.2.3) und (1.2.4) ein, so erhält man:
(1.2.5)
Nun muss noch der Widerstandsbeiwert hinzugefügt werden. Dies ist ein dimensionsloser Proportionalitätsfaktor für den Strömungswiderstand eines Körpers, dessen Größe nur von der Form und der Oberflächenrauhigkeit des umströmten Körpers abhängt und nur Experimentell bestimmt werden kann. Bei einem vernachlässigbar kleinen Reibungswiderstand ist er unabhängig von der Reynoldszahl, beziehungsweiße von der Strömungsgeschwindigkeit. Durch dieses hinzufügen erhält man dann schließlich die Gleichung für die Reibungskraft:
(1.2.6)
Weiterhin gilt diese Gleichung nicht mehr bei hohen Geschwindigkeiten, zum Beispiel nahe der Schallgeschwindigkeit, da dort der Luftwiderstand stärker ansteigt als es der Geschwindigkeit entspricht. Die Reynoldszahl Re bezeichnet das Verhältnis von Zähigkeitskräften zu den Trägheitskräften. Daraus folgt dann auch, dass das Turbulenzverhalten ähnlicher Körper identisch ist, wenn die Re Zahlen gleich sind. Berechnet wird die Reynoldszahl mit der Gleichung:
(1.2.7)
wobei v die Strömungsgeschwindigkeit und d die charakteristische Länge des Körpers ist. Des Weiteren ist die dynamische Viskosität, welche definiert ist als:
(1.2.8)
dabei ist die kinematische Viskosität und die Fluidität, beziehungsweise der Kehrwert der dynamischen Viskosität.
1.3. Bewegungsgleichung und maximale Endgeschwindigkeit
Die Bewegungsgleichung setzt sich zusammen aus der Reibungskraft (1.2.6) und der Gewichtskraft:
(1.3.1)
dabei ist m die Masse des Körpers und g die Erdanziehung. Da die Reibungskraft der Gewichtskraft entgegenwirkt, muss man nun von subtrahieren und man erhält für die wirkende Gesamtkraft die Gleichung Addiert man diese beiden Gleichungen nun, so erhält man:
(1.3.2)
wobei a für die Beschleunigung und t für die Zeit steht. Mittels dieser Gleichung lässt sich nun auch die maximale Endgeschwindigkeit berechnen, indem man setzt und entsprechend umstellt:
(1.3.3)
1.4. Geschwindigkeit und zurückgelegter Weg
Um die Gleichung für die Geschwindigkeit herzuleiten, wird zuerst die Gleichung (1.3.2) nach dt umgestellt und anschließend ausgeklammert:
(1.4.1)
Nun kann man einen Teil der Klammer durch den Kehrwert von ersetzen und erhält so:
(1.4.2)
wobei die Anfangsgeschwindigkeit ist. Wenn man nun im nächsten Schritt [endif]--> durch x substituiert, dann erhält man:
(1.4.3)
Dieses Integral ist nun lösbar
(1.4.4)
dabei muss x² kleiner als eins sein, da man sonst durch null oder einen negativen Betrag teilen müsste, was entweder nicht berechnet werden kann oder zu einem falschen Wert führen würde. Diese Voraussetzung ist allerdings erfüllt, da die Geschwindigkeit v stets kleiner ist als die Endgeschwindigkeit . Die Lösung dieser Differentialgleichung sieht dabei folgendermaßen aus:
(1.4.5)
Da bei auch die Anfangsgeschwindigkeit null ist, muss auch c null sein und da die momentane Geschwindigkeit berechnet werden soll, folgt daraus:
(1.4.6)
Weiterhin gilt:
(1.4.7)
woraus dann auch direkt folgt, dass die Gleichung (1.4.6) gegen den Wert von geht. Den Verlauf einer Tangens Hyperbolicus-Funktion kann man auch in der grafischen Darstellung in Abbildung 1 erkennen. Die Herleitung der Formel für die durchfallene Strecke erfolgt wie bei der Geschwindigkeit, allerdings integriert man dieses Mal die Geschwindigkeit über die Zeit. Dadurch erhält man nun das lösbare Integral:
(1.4.8)
und daraus dann die Gleichung für die durchfallene Strecke:
(1.4.9)
Abbildung 1: Grafische Darstellung der Tangens Hyperbolicus-Funktion
2.1. Ermittlung des Widerstandsbeiwertes
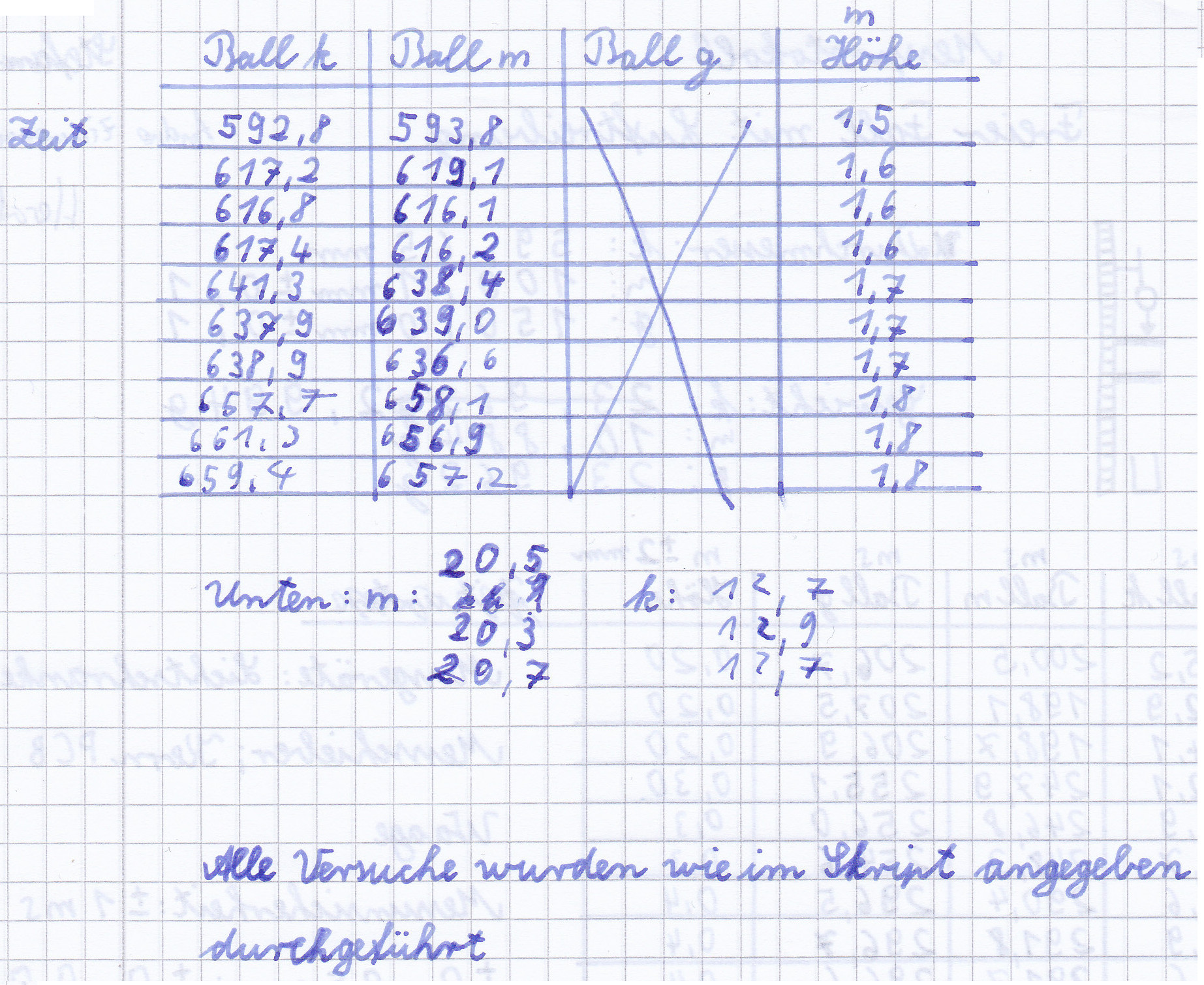
Die Fallhöhe h der Kugeln wurde mit der an der Messvorrichtung befestigten Skala mit einem Fehler von gemessen. Die Fallzeit t wurde mit den Lichtschranken gemessen, wofür ein systematischer Fehler von angenommen wird. Aus den drei, für jede Höhe gemessen Zeiten wird nun der Mittelwert gebildet und anschließend die Fallhöhe über die Fallzeit in einem Diagramm aufgetragen. Für den Fehler der Fallzeit wird nun die größte Differenz zwischen Mittelwert und Messwert der jeweiligen Messreihe verwendet, im Diagramm ist der Fehlerbereich der gemessenen Fallhöhen angegeben durch die Größe der blauen Symbole.
Abbildung 2: Fallhöhe und -zeit der kleinen Kugel
Abbildung 3: Fallhöhe und -zeit der mittleren Kugel
Abbildung 4: Fallhöhe und -zeit der großen Kugel
Nun wurde in Formel (1.4.9) alle Größen eingesetzt und der Wert in einem abgeschätzten Bereich schrittweise variiert. Für die Berechnung wurde die Luftdichte (bei 25 °C) und die Erdbeschleunigung verwendet. Dann wurde für jede Kugel der Wert ausgewählt, bei dem R den kleinsten Wert hat:
, wobei der Index i die verschiedenen Fallhöhen angibt. Anschließen wurde der Fehler für die Werte abgeschätzt, was zu den folgenden Werten führt:
wobei für den Widerstandsbeiwert der kleinen Kugel, für den der mittleren Kugel und für den der großen Kugel steht.
2.2. Berechnung der Reynoldszahl
Die maximale Reynoldszahl wird mit Formel (1.2.7) berechnet:
, wobei die maximale Geschwindigkeit der Kugel ist, welche sie beim Passieren der unteren Lichtschranke hat, und t die Zeit ist, die die Kugel benötigt um die Lichtschranke zu passieren. Für t werden die Mittelwerte aus den drei Messwerten gebildet und dann die Reynoldszahl berechnet:
Damit ergeben sich folgende Reynoldszahlen:
Anhand der folgenden Grafik lässt sich der Wert für die entsprechenden Reynoldszahlen grob ablesen:
Abbildung 5: Widerstandsbeiwert für die entsprechenden Reynoldszahlen [2]
3.1. Diskussion und Vergleich mit Literaturwerten
Die Werte aus 2.1 sind, unter Berücksichtigung der Fehlerbereiche, konsistent mit den Werten aus 2.2 für die kleine und mittlere Kugel, für die große Kugel weicht der Werte aus 2.1 signifikant ab. Die Abweichung nimmt von der kleinen bis zu großen Kugel zu, was sich dadurch erklären lässt, dass die Kugeln eine längere Fallstrecke, bzw. –zeit benötigen um sich ihrer Endgeschwindigkeit anzunähern. Außerdem ließ es der Versuchsaufbau nicht zu, die große Kugel aus einer Höhe, höher als ein Meter fallen zu lassen, was zu weniger Messwerten und somit zu einer geringeren Genauigkeit führte. Zu Beginn des Versuches waren schon deutliche Beschädigungen an den Styroporkugeln zu erkennen, was zu einem verändertem Strömungsverhalten an den Kugeln geführt haben könnte und somit die Messungen deutlich beeinflusst haben könnte.
3.2. Verbesserungsmöglichkeiten
Um die Genauigkeit der errechneten Werte zu erhöhen, könnten mehr Messwerte je Höhe und zusätzliche Höhen erfasst werden. Auch würde der Austausch der bereits leicht beschädigten Styropor-Kugeln, gegen unbeschädigte Kugeln aus einem widerstandsfähigeren Material, die auftretenden Abweichungen minimieren. Des Weiteren könnte durch eine genauere Bestimmung des Kugeldurchmesser und des Kugelgewichtes ebenfalls die Fehlergrößen reduziert werden.
Die in diesem Versuch über die Fallhöhe und –zeit bestimmten Werte lauten:
Die über die maximale Geschwindigkeit und die Reynoldszahl bestimmten -Werte lauten:
- Demtröder, W. (2013). Experimentalphysik 1 - Mechanik und Wärme (6., neu bearbeitete und aktualisierte Ausg.). Springer-Verlag.
- Ghul, R. a. (kein Datum). Wikipedia. Abgerufen am 13. Oktober 2014 von Wikipedia: http://de.wikipedia.org/w/index.php?title=Datei:Kugel-Reynolds.png
- Meschede, D. (2010). Gerthsen Physik (24. überarbeitete Ausg.). Springer-Verlag.
- Tipler, P. A. (2000). Physik (3. korrigierte Ausg.). Spektrum Akademischer Verlag.
- Wikipedia. (kein Datum). Abgerufen am 13. Oktober 2014 von Wikipedia: http://de.wikipedia.org/wiki/Tangens_Hyperbolicus_und_Kotangens_Hyperbo…
- Wikipedia. (kein Datum). Abgerufen am 13. Oktober 2014 von Wikipedia: http://de.wikipedia.org/wiki/Arkustangens_und_Arkuskotangens