Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls A-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Fadenpendel
Inhaltsverzeichnis
2.1. Schwingungsdauer als Funktion der Auslenkung
2.2. Korrekturfaktoren und Reihenentwicklung
2.3. Berechnung der Erdbeschleunigung und deren Fehler
3.1. Diskussion und Vergleich mit Literaturwerten
Eine Schwingung, auch Oszillation genannt, ist eine periodische Bewegung eines Körpers um seine eigene Ruhelage, welche durch eine Auslenkung erzeugt wird. Die harmonische Schwingung ist im Prinzip nur eine reine Sinusschwingung und kann als Projektion einer Kreisbewegung aufgefasst werden.
Das mathematische Pendel Fadenpendel ist ein idealisiertes Fadenpendel, bei dem, ähnlich wie bei dem idealen Gas, verschiedene Näherungen angenommen werden. Diese Näherungen sind einmal die Annahme dass keinerlei Reibung existiert, dass der Faden masselos ist und dass das Pendel eine Punktmasse ist. Die bei einem Fadenpendel wirkenden Kräfte sind in Abbildung 1 grafisch dargestellt, wobei l die Länge des Pendels und der Auslenkwinkel im Bogenmaß ist. Weiterhin existiert die Gewichtskraft , welche mit der Formel:
(1.2.1)
berechnet wird, dabei ist m die Masse des Pendels und g die Erdanziehung. Diese Kraft kann aufgeteilt werden in die Tangentialkraft und die Radialkraft und es gilt weiterhin:
(1.2.2)
Die beiden unterschiedlichen Kräfte werden berechnet mit den Gleichungen:
(1.2.3)
(1.2.4)
d ist dabei die Auslenkung der Kugel zur Ruheposition. Des Weiteren gilt für kleine Winkel die Näherung . Aufgrund des zweiten newtonschen Axioms lässt sich gleichsetzen mit:
(1.2.5)
Weiterhin lautet der Ansatz der Schwingungsdifferentialgleichung:
(1.2.6)
wobei A die Amplitude, die Winkelgeschwindigkeit, t die Zeit und die Phasenverschiebung ist. Wenn man diese Gleichung nun zweimal ableitet und anschließend in (1.2.5) einsetzt, dann folgt daraus die Formel:
(1.2.7)
Dadurch gilt dann für die Schwingungsdauer T:
(1.2.8)
Bei größeren Winkeln muss diese Gleichung allerdings noch geändert werden, da bei diesen die gemachte Näherung nicht mehr gültig ist. Deswegen muss man sie als Reihenentwicklung angeben:
(1.2.9)
Für ein reales Pendel gelten die bei 1.2 gemachten Näherungen nicht, da diese Näherungsannahmen nicht auf die physikalischen Effekte in der Natur übertragen werden können. Deswegen ist es notwendig die Größe der Kugel und die Masse des Fadens zu berücksichtigen und die Gleichungen für das mathematische Pendel entsprechend zu modifizieren. Dazu wird auch der Satz von Steiner, welcher zur Trägheitsmomentberechnung eines starren Körpers dient, benötigt. Er lautet:
(1.3.1)
Dabei entspricht dem Massenträgheitsmoment bezüglich der Achse x, dem Massenträgheitsmoment in Bezug auf einer zu x parallelen Achse durch den Schwerpunkt, m der Körpermasse und dem Abstand der Achse x vom Schwerpunkt S. Daraus folgt dann die Formel für die Schwingungsdauer eines realen Fadenpendels:
(1.3.2)
wobei r der Kugelradius ist. Als letztes muss dann noch, wie bereits erwähnt, die Masse des Fadens mit in die Gleichung eingebracht werden. Wenn man dies nun tut, dann erhält man die Endgleichung für die Schwingungsdauer eines reellen Fadenpendels, welche lautet:
(1.3.3)
dabei ist die Masse der Kugel und die Masse des Fadens.
2.1. Schwingungsdauer als Funktion der Auslenkung
Die Seilmasse und die Seillänge l waren gegeben mit und . Die Kugelmasse m und der Kugelumfang U wurden gemessen zu und . Mit der Lichtschranke wurde die Schwingungsdauer mit einem Fehler von und mit einem Lineal die Auslenkung mit einem Fehler von gemessen. Mit Formel (1.2.2):
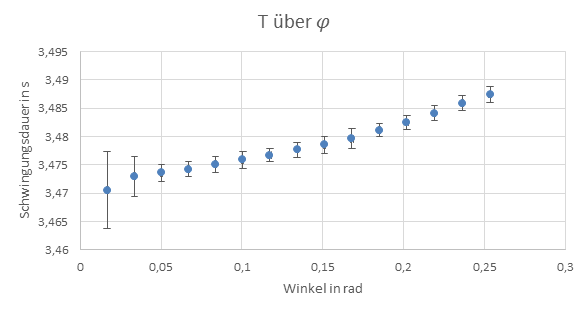
wurden die Winkel für die verschiedenen Auslenkungen berechnet, mit Schwingungsdauer für jede Auslenkung gemittelt und anschließend die Schwingungsdauer als Funktion des Auslenkungswinkels aufgetragen. Beispielrechnung für phi:
Abbildung 1: T über phi
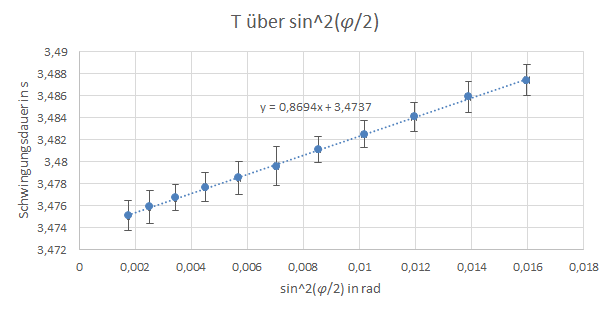
Um , die Schwingungsdauer bei sehr kleiner Auslenkung zu bestimmen wurde nun die Schwingungsdauer als Funktion von aufgetragen. Die ersten vier Messwerte wurden aufgrund ihrer Abweichungen gegenüber den anderen Messwerten für die Bestimmung ignoriert. Aus der Näherungsgeraden kann nun als Achsenabschnitt abgelesen werden.
Abbildung 2: T über sin^2(phi/2)
Dadurch wurde bestimmt zu
2.2. Korrekturfaktoren und Reihenentwicklung
Da in diesem Versuch ein reales Fadenpendel verwendet wurde, müssen die Korrekturfaktoren, welche bereits in den Grundlagen beschrieben wurden, mit einbezogen werden. Dazu wird zuerst der Korrekturfaktor für die Kugel, mittels der Gleichung (1.3.2), ermittelt:
Setzt man nun die gemessenen Werte der einzelnen Größen ein, so folgt daraus:
Des Weiteren muss auch der Korrekturfaktor für den Faden berechnet werden, was mit der Formel (1.3.3) getan wird:
Nun setzt man erneut die gemessenen Werte ein und erhält:
Vergleicht man diese beiden Korrekturfaktoren nun miteinander, erkannt man dass der Fadenkorrekturfaktor stärker von dem Wert eins abweicht, als es der Kugelkorrekturfaktor tut. Die Abweichungen liegen dabei bei und . Da die Abweichung des Korrekturfaktors für die Kugel noch unter der Messungenauigkeit von 0,001 s liegt, ist diese Korrektur vernachlässigbar und nur der Korrekturwert für den Faden von Bedeutung. Weiterhin soll abgeschätzt werden, ob man nach die Reihenentwicklung (1.2.9) nach dem quadratischen Glied abbrechen kann. Dazu wird, ähnlich wie bei der Korrekturfaktorermittlung für die Kugel oder den Faden, T ausgeklammert:
und dann der Korrekturfaktor für das zweite Glied berechnet:
Im Anschluss wird dann für das nächste Glied erneut so vorgegangen:
Die Ergebnisse für die restlichen Korrekturwerte können der folgenden Tabelle entnommen werden:
|
in rad |
in rad |
in rad |
|
0,017 |
1,0000 |
1,0000 |
|
0,033 |
1,0001 |
1,0001 |
|
0,050 |
1,0002 |
1,0002 |
|
0,067 |
1,0003 |
1,0003 |
|
0,084 |
1,0004 |
1,0004 |
|
0,100 |
1,0006 |
1,0006 |
|
0,117 |
1,0009 |
1,0009 |
|
0,134 |
1,0011 |
1,0011 |
|
0,151 |
1,0014 |
1,0014 |
|
0,168 |
1,0018 |
1,0018 |
|
0,185 |
1,0021 |
1,0021 |
|
0,202 |
1,0025 |
1,0026 |
|
0,219 |
1,0030 |
1,0030 |
|
0,236 |
1,0035 |
1,0035 |
|
0,253 |
1,0040 |
1,0040 |
Aus den errechneten Werten kann man entnehmen, dass erst ab größeren Winkeln eine nennenswerte Abweichung entsteht. Da bei den verwendeten Auslenkungen erst ein Unterschied ab der vierten Nachkommastelle entsteht, kann bereits nach dem quadratischen Glied abgebrochen werden. Grund dafür ist, dass die Abweichung noch Unterhalb des Fehlers der Messungenauigkeit von 0,001 s liegt.
2.3. Berechnung der Erdbeschleunigung und deren Fehler
Um aus der Schwingungsdauer die Erdbeschleunigung zu berechnen, muss man einfach nur die Gleichung (1.3.3) nach g umstellen:
(2.3.1)
Fehlerrechnung:
Die Fehler der Korrekturen werden in der folgenden Rechnung nicht berücksichtigt.
Dadurch ergibt sich eine Erdbeschleunigung von:
3.1. Diskussion und Vergleich mit Literaturwerten
Der für die Erdbeschleunigung bestimmte Wert von , welcher in diesem Versuch ermittelt wurde, weicht vom dem in Praktikumsraum angegebenen Wert von bei maximaler Fehlerausnutzung um etwa 0,72% ab. Dies lässt auf kleinere systematische Fehler schließen, bspw. könnte die Auslenkung falsch gemessen worden sein, da sich das Pendel nicht in kompletter Ruhe befand und so das Lineal falsch angelegt wurde. Außerdem konnten die Seilmasse und –länge nicht selbst überprüft werden, sowie der Kugelradius nur indirekt über den Umfang gemessen werden, da der Messschieber nicht ausreichend groß war und kein flexibles Messwerkzeug zur Verfügung stand, sodass die Kugel mit einem Kabel umwickelt werden, und der Umfang am Kabel abgemessen werden musste, was zu weiteren Fehlern geführt haben könnte, wenn die Kugelkorrektur dadurch als Korrekturfaktor relevant werden würde. Des Weiteren wurde die vorhandene Luftreibung nicht berücksichtigt, welche einen nennenswerten Einfluss auf das Messergebnis ausüben wird.
3.2. Verbesserungsmöglichkeiten
Die Aufnahme weiterer Messwerte für jede Auslenkung, würde es ermöglichen einen Mittelwert inklusive Standardabweichung zu ermitteln und so die Genauigkeit der Ergebnisse zu verbessern. Zusätzliche könnten die Messergebnisse verbessert werden, wenn besser geeignete Messgeräte zur Messung des Kugelradius, bzw. –durchmessers, der Seillänge und –masse zur Verfügung ständen.
In diesem Versuch wurde die Schwingungsdauer bestimmt und das mit einem Wert von:
Es wurde außerdem die Erdbeschleunigung in der Universität Kassel bestimmt zu:
Zu deren Berechnung wurden die Korrekturfaktoren der Kugel und des Fadens ermittelt:
Aufgrund der geringen Abweichung durch den Korrekturwert der Kugel, wurde dieser Faktor nicht in die Berechnung mit einbezogen.
- Demtröder, W. (2013). Experimentalphysik 1 - Mechanik und Wärme (6., neu bearbeitete und aktualisierte Ausg.). Springer-Verlag.
- Meschede, D. (2010). Gerthsen Physik (24. überarbeitete Ausg.). Springer-Verlag.
- Tipler, P. A. (2000). Physik (3. korrigierte Ausg.). Spektrum Akademischer Verlag.
- Wikipedia. (kein Datum). Abgerufen am 15. Oktober 2014 von Wikipedia: http://de.wikipedia.org/wiki/Mathematisches_Pendel


unnötiges Protokoll
aAlso dieses Protokoll ist doch reine Verarsche, alles was irgendwie wichtig ist, Formeln, stehen nicht einmal drin!
Die Formeln stehen nicht mehr
Die Formeln stehen nicht mehr drin, da das AddOn zur Anzeige nicht mehr funktioniert und ich noch nicht die Zeit/Lust hatte das zu ändern. Außerdem steht das Wichtigste drin, die Formeln sind nur Beiwerk zum Verständnis.