Dieses Praktikumsprotokoll entstand während meines Physikstudiums im Rahmen des Moduls C-Praktikum. Es wurde von meinem Praktikumspartner und mir erstellt, wobei mein Kommilitone nicht namentlich genannt werden möchte. Das Protokoll wurde zwar testiert, es können sich allerdings dennoch inhaltliche oder grammatikalische Fehler darin befinden. Sollte jemand solche Fehler finden, wäre ich froh wenn er sie mir mitteilt.
Fresnelsche Formeln
Inhaltsverzeichnis
1.1. Reflexion, Brechung und Absorption
2. Auswertung und Durchführung
2.1. Bestimmung des Brewster Winkels
2.2. Bestimmung des Brechungsindexes
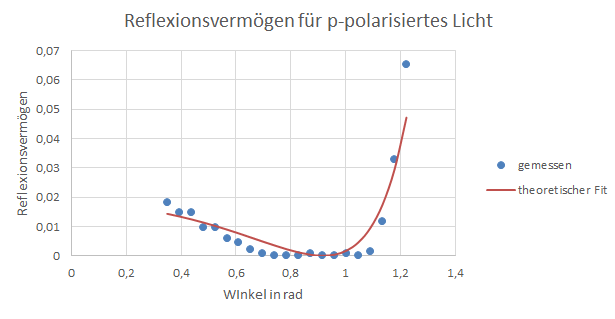
Abbildung 1: Reflexionsvermögen für p-polarisiertes Licht
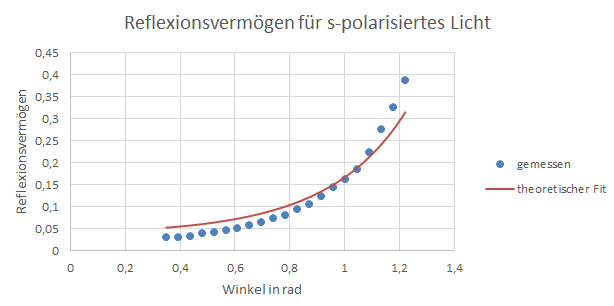
Abbildung 2: Reflexionsvermögen für s-polarisiertes Licht
1.1. Reflexion, Brechung und Absorption
Das Ziels des Versuches ist es sich näher mit den Fresnelschen Formeln, Lichtbrechung, Reflexion, Absorption und Polarisation elektromagnetischer Willen auseinanderzusetzen, sowie mit dem Brewster-Winkel. Wenn Licht auf eine Grenzfläche zwischen zwei Medien mit verschiedenen Brechungszahlen auftrifft, dann wird in den meisten Fällen ein bestimmter Teil des Lichtes reflektiert. Dabei entspricht der Reflexionswinkel dem Einfallswinkel. Der Grund dafür ist, dass die Atomelektronen innerhalb des Mediums durch die Welle des ankommenden Lichtes zum Schwingen gezwungen werden. Dabei wirken sie als schwingende Dipole, weswegen sie dann selbst wiederelektromagnetische Wellen mit der Erregerwellenfrequenz ausstrahlen. Allerdings erfährt dabei die Phase der erzwungenen Schwingung eine Verzögerung gegenüber der Phase der Erregerschwingung. Dies gilt ebenfalls für das Gesamtwellenfeld, da sich dieses aus den beiden Wellen zusammensetzt. Deswegen verändert sich im zweiten Medium auch die Geschwindigkeit des Lichtes. Diese Änderung kann mit der Gleichung:
(1.1.1)
bestimmt werden, wobei c der Lichtgeschwindigkeit im Vakuum, n dem Brechungsindex des Mediums und der Lichtgeschwindigkeit innerhalb dieses Mediums entspricht. Da bei der Brechung sich die Frequenz f nicht ändert, entspricht nun die Wellenlänge des Lichts, welches einfällt, nicht mehr der Wellenlange des transmittierten Lichts. Deshalb gilt nun:
(1.1.2)
(1.1.3)
woraus folgt:
(1.1.4)
Es gilt weiterhin, dass die Stärke der Brechung ist umso größer, desto größer der Einfallswinkel des Lichtes ist. Dabei gilt das Snelliussche Brechungsgesetz:
(1.1.5)
wobei der Einfallswinkel, der Brechungswinkel, der Brechungsindex im Bereich des einfallenden Strahls und der Brechungsindex im Bereich des transmittierten Strahls ist. Dabei werden die Winkel normalerweise zwischen Licht und dem Lot auf die Grenzfläche gemessen. Wenn ein Übergang in ein Medium mit geringerem Brechungsindex stattfindet, dann ändert sich die Ausbreitungsrichtung vom Lot weg und bei einem Übergang in ein Medium mit höherem Brechungsindex zum Lot hin. Der restliche Teil des Lichts hingegen dringt durch die Grenzfläche, man nennt diesen Vorgang auch transmittieren, und wird dabei normalerweise gebrochen. Weiterhin besteht beim Transmittieren die Möglichkeit, dass ein Teil der Intensität verloren geht, dies wird auch als Absorption bezeichnet. Außerdem existieren auch elektromagnetische Wellen, ein Beispiel hierfür wäre Licht, welche eine transversale elektromagnetische Welle ist. Dabei stehen ihre elektrischen und magnetischen Feldstärkevektoren senkrecht sowohl aufeinander als auch auf der Ausbreitungsrichtung. Wobei die Polarisationsebene dem magnetischen Feldstärkevektor zugeordnet wird und die sogenannte Schwingungsebene dem elektrischen Feldvektor . Dabei kann die Polarisation einer elektromagnetischen Welle genau bestimmt werden und zwar mittels der Gleichung:
(1.1.6)
dabei handelt es sich bei um die Kreisfrequenz, t um die Zeit, k um den Wellenvektor, r um den Ort und um die Amplitude. Wenn man jetzt beispielsweise die Wellenausbreitung in Richtung der z-Achse betrachtet, dann findet dabei die Schwingung des Feldvektors nur in einer einzigen Ebene statt. Wenn nun die Wellenkomponente x und y in Phase schwingen, dann handelt es sich um linear polarisiertes Licht und wenn die beiden Komponenten den gleichen Betrag haben:
(1.1.7)
dann existiert eine 90° Phasenverschiebung und es gilt:
(1.1.8)
(1.1.9)
Dadurch wird eine, sich um die z-Achse bewegende, Kreisspirale durch beschrieben, was man auch als zirkular polarisiertes Licht bezeichnet. Außerdem existiert noch elliptisch polarisiertes Licht, welches dann auftritt, wenn:
(1.1.10)
gilt und deswegen eine Phasenverschiebung vorliegt, welche nicht um 90° verschoben ist.
Die Fresnelsche Gleichungen beschreiben die Reflektion und Polarisation von Licht an einer Grenzfläche. Bewegt sich unpolarisiertes Licht, mit dem Einfallswinkel , aus einem Medium mit der Brechzahl in ein anderes Medium mit der Brechzahl , dann tritt ein Teil mit der Intensität B, und dem Brechungswinkel , in das Medium ein und ein gewisser Teil mit der Intensität C wird, mit dem Winkel , an der Oberfläche reflektiert. Dabei werden beide Anteile zum Teil polarisiert. Die Fresnelsche Formeln geben dabei die Amplitudengröße des gebrochenen und reflektierten Lichts bezüglich der Amplitude des einfallenden Lichtes wieder. Dabei beruhen die Fresnelsche Formeln hauptsächlich auf dem Energieerhaltungssatz für die jeweiligen ein- und ausfallenden Wellen und der Stetigkeit der Tangentialkomponente des elektrischen Felds an der reflektierenden Grenzfläche. Dabei sind die Bündelquerschnitte der Wellen gegeben durch:
(1.2.1)
(1.2.2)
(1.2.3)
wobei für die beleuchtete Fläche auf der Grenzfläche, für die Fläche der einfallenden, für die Fläche der reflektierten und für die Fläche der transmittierten Wellen steht. Für den Zusammenhang der Amplituden durch die Stetigkeitsbedingungen an der Grenzfläche siehe Gleichung 1.2.9. Weiterhin wird die räumliche Energiedichte des elektrischen Feldes bestimmt mit ,wobei für die Permittivität steht, und der Energieerhaltungssatz verlangt, dass die Energie der einfallenden Wellen durch die transmittierten und reflektierten Wellen vollständig wieder abtransportiert werden muss. Es gilt also die Gleichung:
(1.2.4)
dabei steht für die Leistung der einfalle, für die Leistung der transmittierten und für die Leistung der reflektierten Wellen. ist aber auch gegeben durch die Formel:
(1.2.5)
wobei für die Strahlungsdichte steht und mittels der Gleichung:
(1.2.6)
berechnet wird. Die Formeln für die Leistungen und erhält man analog und es folgt dadurch:
(1.2.7)
Nimmt man nun als Vereinfachung an, dass die Grenzfläche eben ist, die Medien isotrop, homogen, linear und rein dielektrisch sind, dann kann man Gleichung 1.2.7 vereinfachen zu:
(1.2.8)
wobei für das Verhältnis der Bündelquerschnitte und für den relativen Brechungsindex steht. Weiterhin ist es möglich die elektrischen Feldvektoren in eine senkrecht zur Einfallsebene liegende Komponente und eine parallele Komponente zerlegen. Dabei gilt die Formel:
(1.2.9)
und mit Gleichung 1.2.8 folgt daraus:
(1.2.10)
Aus den beiden Formeln 1.2.9 und 1.2.10 kann man jetzt entweder oder rausstreichen und erhält dann die Fresnelsche Formeln:
(1.2.11)
(1.2.12)
(1.2.13)
(1.2.14)
wobei für die Reflexion und für die Transmission der Amplitudenkoeffizienten steht. Für die parallele Komponente erfolgt die Herleitung analog und man erhält hier die Gleichungen:
(1.2.15)
(1.2.16)
(1.2.17)
(1.2.18)
Linear parallel zur Einfallsebene polarisiertes Licht wird unterschiedlich stark reflektiert, ja nach Grad des Einfallswinkels. Dabei existiert exakt ein Winkel, bei dem es keinerlei reflektierten Anteil gibt, diesen Winkel nennt man Brewster-Winkel oder Polarisationswinkel. Beim Einfallen von unpolarisiertem Licht unter dem Brewster-Winkel wird deshalb nur die senkrecht zur Einfallsebene polarisierten Lichtanteile reflektiert, welche dann dadurch linear polarisiert sind. Der Grund dafür ist, dass die durch das Licht angeregten Elektronen, welche als schwingende Dipole angesehen werden können, nicht mehr längs ihrer Achse emittieren können. Das transmittierte Licht verfügt allerding weiterhin über eine parallelen und eine senkrechten Teil. Da beim Brewster-Winkel der reflektierte und transmittierte Strahl senkrecht aufeinander stehen, gilt die Gleichung:
(1.3.1)
Mittels dieser Formel und 1.1.5 ergibt sich dann:
(1.3.2)
Stellt man diese Gleichung nun nach , welchem hierbei entspricht, um, dann erhält man:
(1.3.3)
2. Auswertung und Durchführung
2.1. Bestimmung des Brewster Winkels
Im ersten Versuchsteil wurde der Objektträger, welcher in diesem Versuch als Glasprisma verwendet wurde in der Halterung des Drehtisches platziert und senkrecht ausgerichtet. Die Anfangsposition des Prismas wurde zu gemessen, sowie der Brewster Winkel durch Drehung des Prismas und Polarisators zu. Für alle mit dem Drehtisch bestimmten Winkel wird ein Fehler von verwendet.
Somit ergibt sich für den Brewster Winkel ein Wert von .
2.2. Bestimmung des Brechungsindexes
Mithilfe des zuvor bestimmten Brewster Winkels und der Annahme, dass der Brechungsindex der Luft ist kann nun der Brechungsindex des Prismas bestimmt werden. Da in Formel (1.1.1) gilt kann sie umgestellt werden zu:
Wird nun und verwendet, so kann der Brechungsindex des Prismas bestimmt werden:
Daraus ergibt sich nun der Brechungsindex von .
2.3. Bestimmung des Reflexionsvermögens
Aus Formeln (1.2.11) bzw. (1.2.15) und dem Zusammenhang, welche analog für parallel polarisiertes Licht gilt, kann das Reflexionsvermögen aus den Messwerten der vom einfallenden und reflektierten Licht an der Photozelle erzeugten Spannungen berechnet werden. Außerdem können mit (aus dem Brechungsgesetz) und der Näherung die Formeln der theoretischen Reflexionsvermögen umgeschrieben werden zu:
Zuerst wurde die Intensität des reflektierten p-polarisierten Lichts unter einem Einfallswinkel von 20° gemessen. Der Winkel wurde bis 70° in Schritten von 2,5° variiert und anschließend die Messung ebenfalls für s-polarisiertes Licht durchgeführt, indem der Polarisator um 90° gedreht wurde. Die Berechnung des Reflexionsvermögens wird hier beispielhaft für die erste Messung durchgeführt.
Nun werden mit den zuvor genannten Formeln der theoretischen Reflexionsvermögen über den Parameter Fit-Funktionen erstellt. In den folgenden zwei Diagrammen wurden die berechneten und angefitteten Werte des Reflexionsvermögens aufgetragen.
Abbildung 1: Reflexionsvermögen für p-polarisiertes Licht
Abbildung 2: Reflexionsvermögen für s-polarisiertes Licht
Für den angefitteten Parameter ergibt sich bei p-polarisiertem Licht und bei s-polarisiertem Licht . Da bei dem Brewster Winkel das Reflexionsvermögen für p-polarisiertes Licht am niedrigsten ist kann der Brewster Winkel am Minimum der Funktion abgelesen werden. Das Minimum der Fit-Funktion befindet sich bei .
Der Brechungsindex von Glas liegt nach Literaturwerten zwischen 1,44 und 1,95, demnach befindet sich nur der Brechungsindex welcher über die Fit-Funktion des p-polarisierten Licht außerhalb dieses Intervalls. Die Werte für Kronglas FK 3 [4] mit und weichen nur minimal von den experimentelle bestimmten Werten des Brechungsindexes und des Brewster Winkels ab. Der aus dem Brewster Winkel bestimmte Brechungsindex von stimmt zwar nicht mit den einzelnen gefitteten Werten von und überein, liegt aber zwischen beiden. Anhand der Diagramme wird bereits deutlich, dass die experimentellen Werte, besonders beim p-polarisierten Licht, zwar immer noch dem allgemeinen Trend folgen, teilweise aber deutlich von den theoretischen Werten abweichen. Fehler bei der Messung könnten dadurch aufgetreten sein, dass Licht benötigt wurde um die Messwerte abzulesen. Auch war bei der Bestimmung des Brewster Winkels trotzdem noch etwas Licht zu sehen, sodass dieser vermutlich nicht genau eingestellt wurde. Um den Polarisator später um 90° drehen zu können wurde auf einem Blatt Papier die Form des reflektierten Lichts an der Wand markiert , das Blatt um 90° gedreht und anschließend die Form des Lichts durch Drehen des Polarisators wieder an der Markierung ausgerichtet, was wahrscheinlich nicht alles fehlerfrei erfolgt ist. Bei p-polarisiertem Licht war es in dem Bereich um den Brewster Winkel aufgrund des nur sehr schwachen reflektierten Lichts schwer möglich zu beurteilen, ob das reflektierte Licht genau auf der Photozelle auftrifft, weshalb durch die fehlerhafte Ausrichtung die gemessene Spannung in dem Bereich um den Brewster Winkel nahezu konstant 0 ist. Alle Ausrichtungen und Drehungen erfolgten von Hand, weshalb der Fehler hätte verringert werden können, wenn z.B. die Drehung des Polarisators elektrisch gesteuert worden wäre.
In diesem Versuch wurde Brewster Winkel gemessen zu
und über die Fit-Funktion bestimmt zu
.
Der Brechungsindex des Prismas wurde experimentell bestimmt zu
sowie über zwei Fit-Funktionen zu
und
- Demtröder, W. (2009). Experimentalphysik 2 - Elektrizität und Optik (5. überarbeitete und erweiterte Ausg.). Kaiserslautern: Springer-Verlag.
- Eisenhut, C. (6. Mai 2015). Lernort-Mint. Abgerufen am 6. Mai 2015 von Lernort-Mint: http://www.lernort-mint.de/Physik/Optik/lichtberechung_an_grenzen.html
- Forster, M., & Steinbach, S. (6. Mai 2015). ChemgaPedia. Abgerufen am 6. Mai 2015 von ChemgaPedia: http://www.chemgapedia.de/vsengine/vlu/vsc/de/ph/14/ep/einfuehrung/well…
- Kuchling, H. (2014). Taschenbuch der Physik (21. Auflage Ausg.). München: Carl Hanser Verlag.
- Tipler, P. A., & Mosca, G. (2009). Physik (6. Ausg.). Springer-Verlag.